¿Qué es la Serie de Fibonacci?
Las series de Fibonacci fueron bautizadas en honor del italiano por el teórico francés Edouard Lucas, porque este tipo de sucesiones numéricas forman parte de un problema bastante sencillo del Liber abaci.
La secuencia( o serie) de Fibonacci es una secuencia infinita de número que comienza por: 1, 1, 2, 3, 5,8,13…, en la que cada uno de ellos es la suma de los dos anteriores,respondiendo a la fórmula
Fn = Fn-1 + Fn-2
Lo interesante de las series de Fibonacci es que prácticamente cualquiera (con la sola condición de que domine la aritmética básica) puede investigarlas, descubrirles nuevas propiedades y desarrollar teoremas propios, inéditos y curiosísimos sobre ellas. Parecen existir infinitos teoremas de Fibonacci, y amateurs matemáticos casi absolutos han escrito y publicado interminable cantidad de sesudos libros acerca de ellos.r
Así: 2=1+1, 3=2+1, 5=3+2, 13=8+5 . Para cualquier valor mayor que 3 contenido en la secuencia, la proporción entre cualesquiera dos números consecutivos es 1,618, o Sección Áurea.
La secuencia de Fibonacci se puede encontrar en la naturaleza, en la que la flor del girasol, por ejemplo, tiene veintiuna espirales que van en una dirección y treinta y cuatro que van en la otra; ambos son números consecutivos de Fibonacci.
Girasol, la flor mágica y la serie de Fibonacci

Los caparazones espirales de muchos caracoles se rigen por esta sucesión, como ciertas proporciones de la anatomía humana, animal y vegetal. También se han hallado manifestaciones de estas entidades en las artes plásticas, la arquitectura y la poesía. Varios bardos romanos, especialmente Virgilio en la Eneida, parecen haber utilizado las series de Fibonacci en la estructura de sus obras poéticas.
FILOTAXIA
La parte de la botánica que estudia la disposición de las hojas a lo largo de los tallos de las plantas se denomina Filotaxia. En la mayoría de los casos es tal que permite a las hojas una captación uniforme de la luz y aire, siguiendo, normalmente, una trayectoria ascendente y en forma de hélice.

Si tomamos la hoja de un tallo y contamos el número de hojas consecutivas (supongamos que son ‘n’) hasta encontrar otra hoja con la misma orientación, este número es, por regla general, un término de la sucesión de Fibonacci. Además, si mientras contamos dichas hojas vamos girando el tallo (en el sentido contrario a las agujas del reloj, por ejemplo) el numero de vueltas ‘m’ que debemos dar a dicho tallo para llegar a la siguiente hoja con la misma orientación resulta ser también un término de la sucesión.
Pues bien, se llama “característica” o “divergencia” del tallo a la fracción m/n, y que, como muestra en la figura 2,
en el olmo es 1/2, en el álamo 2/5, en el sauce llorón 3/8 y en el almendro 8/13.
Si representamos por Fn el término que ocupa el lugar ‘n’ en la sucesión de Fibonacci (consideremos, por ejemplo: F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13), en la mayoría de los casos la característica viene dada por una fracción del tipo Fn/Fn+2. Así, en el caso del sauce llorón sería F4/F6.

Las “hojas” de una piña de pino tienen, por regla general, una característica de 5/8 o bien 8/13, presentando propiedades similares las hojas de las lechugas, los pétalos de las flores, las ramas de las palmeras, el ficus, etc., ejemplos que se pueden comprobar fácilmente.
La parte externa de una piña piñonera tiene espirales que van en sentido de las manecillas del reloj y otras que lo hacen en sentido contrario, y la proporción entre el número de unas y otras espirales tiene valores secuenciales de Fibonacci.
Piña y Sucesión de Fibonacci, –http://www.maikelnai.es/wp-content/uploads/2007/09/pina-fibonacci.gif-
En las elegantes curvas de una concha de nautilus, cada nueva circunvolución completa cumplirá una proporción de 1: 1,618, si se compara con la distancia desde el centro de la espiral precedente.
Las abejas también tienen relación con las series de Fibonacci: si se observan las celdas hexagonales de una colmena y se coloca una abeja en una cualquiera de ellas, y se le permite alimentar a la larva, suponiendo que continuará siempre por la celda contigua de la derecha, veremos que hay sólo una ruta posible para la siguiente celdilla; dos hacia la segunda, tres hasta la tercera, cinco hasta la cuarta, ocho rutas posibles hacia la quinta, etcétera.
1, 1, 2, 3, 5, 8
¿Cuantos habrá hacia la sextaaaa?

Y, ya que estamos a ello, diremos que los machos o zánganos de la colmena tienen árboles genealógicos que siguen estrictamente una distribución de Fibonacci.
Genealogía
El número de descendientes en cada generación de una abeja macho o zángano nos conduce a la sucesión de Fibonacci, y por lo tanto, al número áureo.

: http://www.juntadeandalucia.es/averroes/recursos_informaticos/concurso2002/alumnado/naturaleza.html

En efecto, los machos no tienen padre, por lo que él (1), tiene una madre (1, 1), dos abuelos —los padres de la reina— (1, 1, 2), tres bisabuelos —porque el padre de la reina no tuvo padre— (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5) y ocho tataratatarabuelos (1, 1, 2, 3, 5, 8).
EL HOMBRE

Leonardo Da Vinci realizó este dibujo para ilustrar el libro De Divina Proportione del matemático Luca Pacioli editado en 1509. En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean las del dibujo adjunto. Resulta que la relación entre la altura del hombre y la distancia desde el ombligo a la mano es el número áureo.

En el cuerpo humano el número áureo aparece en muchas medidas: la relación entre las falanges de los dedos es el número áureo, la relación entre la longitud de la cabeza y su anchura es también este número.
La mano humana es, también, una serie de Fibonacci.
La longitud del metacarpo es la suma de las dos falanges proximales;
la longitud de la primera falange es la suma de las dos falanges distales
Si aumentamos el número de reflexiones (n), el número de trayectorias posibles sigue infinitamente una serie de Fibonacci.
Si se toma un grupo de fichas de dominó, de tamaño 2 x 1, la cantidad de maneras de construir rectángulos de tamaño 2 x n será, por supuesto, una serie de Fibonacci. Hay una sola forma de armar un rectángulo de 2 x 1; dos de construir el de 2 x 2; tres de hacer el de 2 x 3, cinco para el de 2 x 4; ocho para el de 2 x 5, etc.
Desde siempre, los matemáticos se vieron perturbados por la relación entre las series de Fibonacci y las de números primos. La pregunta era: ¿puede una sucesión de Fibonacci contener series infinitas de números primos? La respuesta es sí. Si construimos una serie de Fibonacci general, en la cual los dos primeros números son divisibles por un número primo, todos los subsiguientes serán divisibles por el mismo primo a su vez, y toda la serie, por grande que sea, no podrá contener más que un número primo. Esto se conoce desde la Antigüedad.
Verduras de Fibonacci
El postulado negativo era más difícil de probar: ¿Puede existir una serie de Fibonacci que no contenga ningún número primo? Hubo que esperar a que modernamente se inventaran las computadoras para responder a este interrogante. La respuesta es sí. Pueden existir series de Fibonacci sin números primos en absoluto, de hecho existen, y parece haber también una variedad infinita de ellas. Pero no están cerca de nuestra simple serie de números bajos 1, 1, 2, 3, 5… La más pequeña de las series de Fibonacci sin números primos comienza en
1.059.683.225.053.915.111.058.165.141.686.995
y concluye en
1.786.772.701.928.802.632.268.715.130.455.793.
Las peculiaridades de las series de Fibonacci son, en apariencia, infinitas. Son tan atractivas que es fácil caer encandilados bajo su hechizo.

Leonardo Fibonacci o de Pisa
Leonardo nació en Pisa. Italia, en 1170. Creció y fue educado en Bugia, norte de África (hoy llamada Bejaia, en Argelia), desde donde regresó a Pisa alrededor del año 1200. Fihonacci fue sin duda influido y posiblemente enseñado por matemáticos árabes durante este su periodo más formativo. Escribió muchos textos matemáticos e hizo algunos descubrimientos matemáticos significativos, lo que ayudó a que sus trabajos fueran muy populares en Italia y a que le prestara atención el Sacro Emperador Romano del momento Federico II, quien lo invito a su corte de Pisa.
Fibonacci, el hijo de Bonaccio, también conocido como Leonardo de Pisa, nació en esta ciudad italiana a finales del siglo XII. Su padre, director de una aduana italiana en Argelia, le obligó a estudiar aritmética posicional hindú, pero no podía sospechar que su hijo iba a hacer de las matemáticas su vida.

Pues bien, Fibonacci, recordando el curso de aritmética hindú aprendido de niño, escribió en 1202 su tratado Liber abaci (”El Libro del Ábaco”) que es, ni más ni menos, un tratado sobre el sistema numeral indoarábigo. En él presenta al público y a los científicos europeos los signos hindúes (1, 2, 3…) y el 0 árabe, donde dice que se llama “cero” (quod arabice zephirum appellatur). Además, expone el método de regula falsi para ecuaciones de primer grado. Nada menos que eso, algo insólito para un libro del siglo XIII en una sociedad que no usaba el cero.
Su otro libro capital, De quadratis numeris (1225) es tan avanzado que hubo que esperar a Fermat (en el siglo XVII) para superarlo.
En la época en la que vivió, todo el mundo usaba el sistema de numeración romano y la manipulación de los números con el nuevo sistema que estaba desarrollando, el sistema numerico indoarábigo, que es el que usamos ahora, permitió avanzar muchísimo más rápido. Además, trajo a Europa el cero, quod arabice zephirum appellatur, lo cual supuso, como todos sabemos, una revolución.


centros5.pntic.mec.es/…/Fibonnacci.htm
Fibonacci fue sin duda el matemático más original y hábil de toda la época medieval cristiana, pero buena parte de sus trabajos eran demasiado difíciles para ser bien comprendidos por sus contemporáneos.
Fibonacci murió en 1250.
Sucesión de Fibonacci
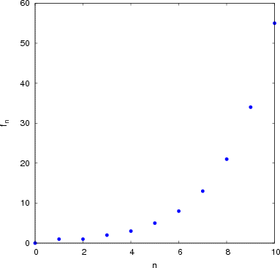
En matemáticas, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales:Los primeros términos de esta sucesión son:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309…
Serie de Fibonacci y proporción áurea.Wikipedia
Una de las características de la serie de Fibonacci es que, a medida que n aumenta, la relación entre dos términos sucesivos tiende a Φ, siendo este el valor de la proporción áurea.
La proporción áurea es una relación entre longitudes tal que
a/b = b/(a − b)
Se representa con la letra griega Φ, su valor exacto es
Φ = 1/2 · (1 + √5)
y su valor aproximado
Φ ≈ 1,618…
Oservemos la siguiente figura. En ella vemos un rectángulo ABCD. Este rectángulo se ha construído de forma tal que AD = ΦAB y se denomina rectángulo áureo. Se ha dividido el segmento AD por el punto F, de tal forma que FD = AB y, en consecuencia, FD = ΦAF. De esta forma, el rectángulo ABEF es también un rectángulo áureo, así como el BEHG, el EHJI y los sucesivos obtenidos de la misma forma.
Apoyándose en los puntos C, F, G, I… se obtiene la llamada espiral áurea, que es un caso particular de las espirales logarítmicas.
Curiosidades de Fibonacci:
Fibonacci utilizaba las matemáticas planteándolas como problemas diarios como en el famoso problema de los conejos de Fibonacci: partiendo de una pareja de conejos queremos saber la cantidad de conejos que habrá a lo largo de cada generación; es un problema que sobresale por su enorme longevidad. Son muchos los matemáticos que han trabajado sobre el problema y que siguen trabajando, y es rara la revista matemática que no le haya dedicado alguna vez un artículo.
El problema en detalle es el siguiente: ¿cuántas parejas de conejos tendremos a fin de año si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida? El número de parejas que hay al terminar cada mes es una sucesión en la que cada término es la suma de sus dos precedentes,1,1,2,3,5,8,13,21,34,55,89,144



Fuentes consultadas:
http://www.sectormatematica.cl/biografias/fibonacci.htm
Proporción áurea y naturaleza.La mano, sus huesos y la Serie de Fibonacci
http://www.digtv.es/dig/imagen/NUMERO%20MAGICO/ilustracion.jpg
Existen muchas formas de representar la proporción exacta o divina a través del diseño de nuestro propio Universo y en muchas cosas que nos rodean, pero centremonos en algo tan básico y cercano como tú mismo. En matemática esta proporción exacta está representado por el número de Fibonacci, que es 1.618. La serie Fibonacci también es muy conocida y se saca de sumar al número actual, el precedente para sacar el siguiente, empezando por 1, es decir, que la serie sería: 1, 1, 2, 3, 5, 8, 13, 21…

Algo tan sencillo como tu mano. Mira fíjamente el tamaño de tu dedo índice. Pon tu dedo en la pantalla junto a la imagen para hacerlo más fácil. Cada sección de tu índice, desde la punta a la base de la muñeca es más largo que el que le precede en una proporción exacta al número de Fibonacci, que es 1.618, tal y como se ve en la figura. La uña es como si fuera la “unidad” desde donde contar todo lo demás.
Pero curiosamente, tienes 2 manos, cada una con 5 dedos, y tus 8 dedos (sin contar los gordos) constan de 3 secciones. Todos los números son parte de la serie de Fibonacci. La proporción entre tu antebrazo y tu mano también es Phi (1.618).
Pero no sólo en nuestro cuerpo existen estas proporciones exactas (o aúreas) que muy bien representó Leonardo Da Vinci en su hombre de Vitrubio, sino que en la naturaleza hay otros muchos casos como la cantidad de pétalos de una flor, la cantidad de espirales en una piña, la manera de reproducirse las liebres-o conejos, la cantidad descendientes que tienen y como se “multiplican”, o simplemente la relación entre altura y anchura de una tarjeta de crédito.
Es impresionante la cantidad de “perfección” que hay en la naturaleza.

La proporción áurea es el límite en el infinito de la sucesión de Fibonacci. Por diferentes razones, esta serie es, para los seres vivos, una forma muy eficiente de crecer (a groso modo, consiste en añadir a dos elementos ya existentes uno de tamaño igual a la suma de ambos), por lo que es muy frecuente encontrar esta proporción en los seres vivos.
Proporción áurea y arte.
El número áureo o de oro (también llamado número dorado, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en honor al escultor griego Fidias), es el número irracional:

Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción.
Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Asimismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología.
![[Serie+de+fibonacci.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhIMkfmXcmZctIdAh3lwQ6DdFwwV9fQrI7wVYEb3K-AZ7fdu3fZdaIdWLIn6mmxzFzhE-8dOEYXtXt5Njrt1GPMqB3UeyyX75CgeFAGqPHTs6PWExHsfTNj6WBc-RSd3flxobYLTCuob1k/s1600/Serie+de+fibonacci.jpg)
La proporción áurea es especialmente atractiva para el ser humano. Muchos artístas en diferentes épocas y culturas han recurrido a ella, a veces de forma inconsciente, pues da lugar a obras que resultan estéticas.
NÚMERO DE ORO EN EL ARTE

El número áureo ha sido utilizado desde la época de los egipcios para la construcción de edificios, si bien, son los griegos los que lo explotaron al máximo usando en todas las facetas del arte. A continuación se detallan algunos ejemplos de este uso:
Pirámide de Keops
El Primer uso conocido del número áureo en la construcción aparece en la pirámide de Keops, que data del 2600 a.C..
Esta pirámide tiene cada una de sus caras formadas por dos medios triángulos áureos: la más aparente, aunque no la única, relación armónica identificable en el análisis de las proporciones de este monumento funerario en apariencia simple.
Pirámide de Keops

El primer uso conocido del número áureo en la construcción aparece en la pirámide de Keops, que data del 2600 a.C..

Esta pirámide tiene cada una de sus caras formadas por dos medios triángulos áureos: la más aparente, aunque no la única, relación armónica identificable en el análisis de las proporciones de este monumento funerario en apariencia simple.
El Partenón
Un ejemplo de rectángulo áureo en el arte es el alzado del Partenón griego.
En la figura se puede comprobar que AB/CD=. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=.
El Templo de Ceres

El Templo de Ceres en Paestum (460 a.C.) tiene su fachada construida siguiendo un sistema de triángulos áureos, al igual que los mayores templos griegos, relacionados, sobre todo, con el orden dórico.
Tumba Rupestre de Mira

La Tumba Rupestre de Mira en Asia Menor basa su construcción en un pentágono áureo, en el que el cociente de la diagonal y el lado de dicho pentágono es el número áureo.
El número áureo ha sido utilizado desde la época de los egipcios para la construcción de edificios, si bien, son los griegos los que lo explotaron al máximo usando en todas las facetas del arte. A continuación se detallan algunos ejemplos de este uso.
El Partenón

Un ejemplo de rectángulo áureo en el arte es el alzado del Partenón griego.
http://www.juntadeandalucia.es/averroes/recursos_informaticos/concurso2002/alumnado/construcciones.html

En la figura se puede comprobar que AB/CD=
 . Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD=
. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=
y CD/CA= .
.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … | … |
| F(n) | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … | … |
| F(n)/F(n-1) | 1 | 2 | 1,5 | 1,666… | 1,6 | 1,625 | 1,615… | 1,619… | … | Φ ≈ 1,618… |
La Serie de Fibonacci en movimiento